Doğada gizlenen oran: altın oran
İnsanoğlu tarihler boyunca etrafında var olan nesneleri incelemiş ve özelliklerini belirlemeye çalışmıştır. Bu uğraşlar içerisinde en büyük yardımı ise matematikten ve fizyolojiden almıştır. Tüm bu çalışmalar sonucunda ise “altın oran” olarak tanımlanan bir kavramın farkına varılmıştır. Altın oran, diğer bir deyişle altın kesit kavramı yaygın biçimde doğada, klasik sanatta, modern mimaride, bilimde ve son yıllarda beyinle ilgili yapılan araştırmalarda beyindeki biliş (cognition) sisteminde de temel rol oynayan bir kavramdır. Bu kavram evrenin varoluşundan itibaren mevcut, temel bir unsur olmakla birlikte ilk olarak Orta Çağ’da altın oran adıyla kullanılmaya başlanılmıştır. Aslında doğada gizlenen bu oran yani altın oran kavramı milattan önceki çağlardan beri bilinmekteydi. Örneğin Firavun zamanında Mısır’daki bilim adamları ve sanatçılar insan anatomisindeki orantıyı fark etmişler ve piramitlerin inşasında bu ölçüyü baz almışlardır. Yine M.Ö. 5.yüzyılda ünlü heykeltıraş Polyklet insan vücudunun orantısal yapısıyla ilgili bir kitap yayınlamıştır [1]. En özet biçimde altın oran
değerinde bir sayıdır. Aynı zamanda,
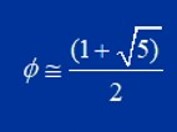
şeklinde de ifade edilebilir. Altın oranla ilgili matematiksel bir dizi, halk arasında Pisalı Leonardo olarak bilinen 1175 doğumlu Leonardo Fibonacci (Fillus Bonacci) tarafından tanımlanmıştır. Bu dizinin her bir terimi kendisinden önce gelen ilk iki terimin toplamı olarak tanımlanmaktadır [2-6].
Fibonacci serisi:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946…
Bu dizinin en önemli tarafı 5.terimden sonra ardışık terimlerinin oranlarının altın orana çok yakın olmalarıdır. 1/1=1; 2/1=2; 3/2=1,5; 5/3=1,666; 8/5=1,6; 13/8=1,625; 21/13=1,615; 34/21=1,619…12.terim olan 144 sayısından sonraki bütün ardışık terimlerin oranı ise sürekli olarak yaklaşık 1,618’dir yani altın orandır [2-6].
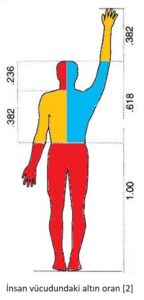Yukarıdaki resim boyu yaklaşık 162 cm olan bir insan için örneklendirilmiştir. Fakat asıl oran aşağıdaki formüllerle bulunur;
Boy / Bacak Boyu= f Beden Boyu / Kolaltı Beden Boyu= f Tam Kol Boyu(Boyun-parmak ucu) / Dirsek-Boğaz= f
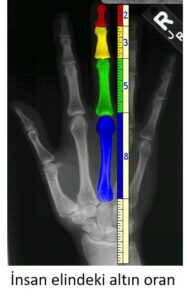Fibonacci 1202 yılında yazdığı “Liber Abaci” adlı matematik kitabıyla Avrupa’ya Hint-Arap sayı sistemini ve o zamana kadar sadece Hint-Arap sayı sistemleri tarafından bilinen ve kullanılan sıfır sayısını tanıtmıştır. Fakat asıl ününü kitabında değindiği Fibonacci sayı dizisi ve doğadaki karşılıklarıyla kazanmıştır [4-7].
Fibonacci dizisi doğada çok sık bir biçimde karşımıza çıkmaktadır. Örneğin çam kozasında, papatya tomurcuklarında, ay çiçeklerinde, tavşanların hangi düzene göre üredikleri konusundaki bilgiye kadar bu dizinin oranlarını görmekteyiz [2-6]. Doğadaki oluşumlarda meydana gelen anlık büyümeler veya küçülmeler, örneğin bir ağacın veya bitkinin büyümesindeki ani değişiklikler, zaman ya da doğadaki karşılığı olan sıcaklık kavramıyla özdeşleştirilebilir. Bu ani değişiklikler nedeniyle altın oranın doğadaki tezahürü 1,618 sayısının virgülden sonraki dördüncü veya daha sonraki basamaklarında farklılıklar oluşturabilmektedir.
Özellikle, papatya çiçeği ortasındaki sarmalların sayısının iki ardışık Fibonacci sayısına eşit olduğunun saptanması sonucu konunun ilginçliği nedeniyle 1962’de California’da bir Fibonacci Derneği kuruldu. Bu tarihten bugüne kadar geçen yaklaşık 45 yılda, bilimde ulaşılan yerden olaya bakıldığında, beyin ile ilgili araştırmalar sonucu, insanın beynindeki biliş (cognition) mekanizmasında da, Fibonacci serisindeki sabit sayıya eşit bir frekansın temel rolü oynadığının anlaşılması şeklinde özetlenebilir [8,9].
Beyin tarafından bilgi kodlama prensibi, altın oran esasına dayanmaktadır. Altın oran değerinin (1,618) beyin için önemli bir rezonans frekans değerine eşit olduğu anlaşılmıştır. Son yıllarda özellikle psikologların ölçülebilen zekâ ile beyindeki biliş mekanizması arasında eksik olduğu ifade edilen bir unsurun öğrenme deneylerine ait sisteme, Bose-Einstein dağılım istatistiğini ithal etmek suretiyle bulunmuş olduğu ifade edilmektedir. Böylece, ölçülen ile öngörülen arasındaki uyumsuzluk giderilerek örtüşme sağlanır[10].
Kuantum mekaniksel dalga paketleriyle betimlenen beyin dalgalarına ait paketlerin altın oran sayısının kuvvetleriyle betimlendiği; böylece uzayda yönü olan sayılar sistemi elde edildiği anlaşılmıştır. [8]
Sonuç olarak, doğada fiziksel olarak mevcut olan altın oran kavramı, beyindeki biliş sisteminde de ortaya çıkarak bizlere yeni ufuklar açabileceği söylenebilir.
Prof. Dr. Özden Aslan Çataltepe
Kaynaklar
[1]Emre Becer, Biçimsel Uyumun Matematiksel Kuralı Olarak Altın Oran, Bilim ve Teknik, Ocak 1991, Syf 18
[2]Öner Çakar, Doğanın Güzellik Ölçüsü, Bilim ve Teknik, Ağustos 1992, Syf 6
[3]Bilim ve Teknik, Matematiğin Şaşırtan yüzü: Fibonacci Sayıları, Syf 108, Kasım 2003
[4]http://en.wikipedia.org/wiki/Fibonacci_number
[5]http://goldennumber.net/fibonser.htm
[6]http://www.biltek.tubitak.gov.tr/gelisim/matematik/sayilar.htm
[7]http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html
[8]H. Weiss and V.Weiss; “The Golden Mean as Clock Cycle of Brain Waves”, Chaos Solitons and Fractals, 18 (2003)643-652
[9] Ana Britannica vol.A
[10] U.Onbaslı, Özden Aslan, Zeynep Güven Özdemir, Olasılık Yoğunluğu Kavramındaki Süper Mantık, Mantık, Matematik ve Felsefe IV Ulusal Sempozyumu, Olasılık, 05-08 Eylül 2006, Foça-İzmir, İstanbul Kültür Üniversitesi Yayınları, Olasılık, 2008, Syf 79-90.